Important About Undercomplete Autoencoder
Autoencoders in a broader sense
If we were to sum them up in a single statement, it would probably go like this:
Yes, it may appear to be simple and pointless. We will see, however, that this is not trivial nor insignificant. Autoencoders, in reality, are deep models that can learn dense representations of the input. Latent representations or coding are the names given to these representations.
There are two pieces to an Automatic encoder:
An encoder: It is a component of the model that accepts input data and compresses it. Where x is the input data, c is the latent representation, and E is our encoding function, E(x) = c
A decoder: This component accepts the latent representation as a parameter and attempts to recreate the original input. D(c) = x’, where x’ is the decoder’s output and D is our decoding function
What is an enactment capability in a brain organization?
We utilize the Enactment Capability to accomplish non-linearity. For instance,we can take care of any information into it.
A nonlinear capability is utilized to accomplish the upsides of a multi-facet organization. …
On the off chance that we don’t matter the enactment capability then the result would be a direct function,and that will be a Straightforward Straight Relapse Model.
Undercomplete Autoencoder
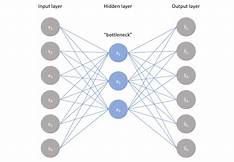
Our network should be able to learn how to reassemble our input data throughout the training phase. The Autoencoders model architecture is shown in the following diagram to demonstrate this concept.
The latent space representation, rather than the decoder’s output, is what we’re interested in most of the time. We expect that by fully training the Automatic encoder, our encoder will be able to detect valuable characteristics in our data.
The decoder is used to train the Autoencoders from beginning to end, although in practice, we are more concerned with the encoder and coding.
One might, for example, confine the latent space to be smaller than the dimension of the inputs to emphasize crucial qualities. Our model is an Undercomplete Autoencoders in this circumstance. We use this form of automatic encoder in the majority of situations since dimensionality reduction is one of the keys uses of this architecture.
The learning process is quite consistent, with the goal of reducing a loss function.
Different metrics, such as the Mean Square Error or cross-entropy, can be used to characterize this loss function (when the activation function is a sigmoid for instance). Because the reconstruction is different from x, this loss must punish it.
Principal Component Analysis with Linear Autoencoders
As a result, dimensionality reduction is one of the keys uses of Automatic encoders, similar to Principal
Component Analysis (PCA). In reality, an Autoencoder learns to span the same subspace as the PCA if the decoder is linear and the cost function is the Mean Square Error.
PCA: By measuring and decreasing the distance between input data and its reconstruction, we may reduce the gap between the two. (Take, for instance, the Euclidian distance.)
N.B. The decoding matrix’s vectors must have unit norms and be orthogonal.
Singular Value Decomposition can be used to tackle this optimization challenge. The eigenvectors of the X covariance matrix corresponding to the greatest eigenvalues provide the optimum P. Again, that property’s comprehensive presentation is outside the scope of this lesson.
Autoencoders: If we choose to train them using the Mean Square Error, we want to reduce the error as much as possible.
more like this, just click on: https://24x7offshoring.com/blog/
The loss function becomes the loss function when f and g are linear.
Both strategies have the same convex objective function, but they get at it in two distinct ways.
In actuality, automatic encoders are feedforward neural networks that have been trained using techniques like Stochastic Gradient Descent.
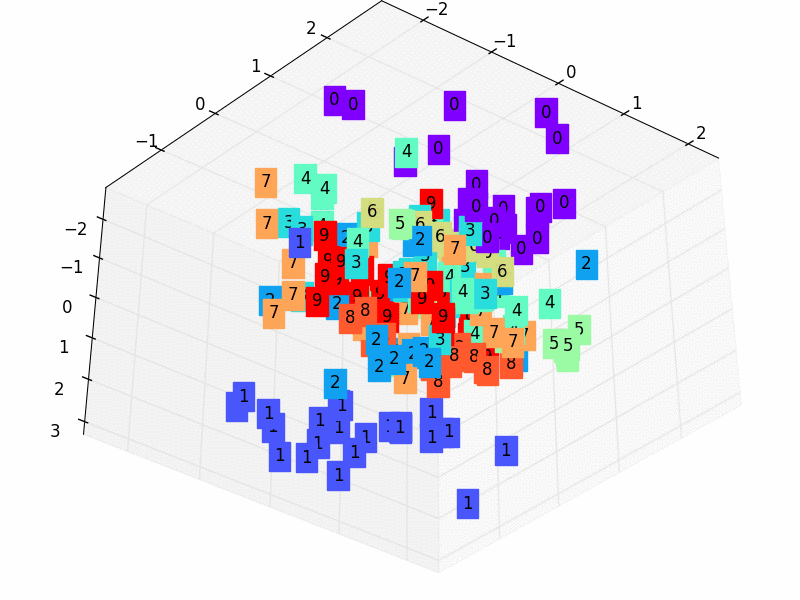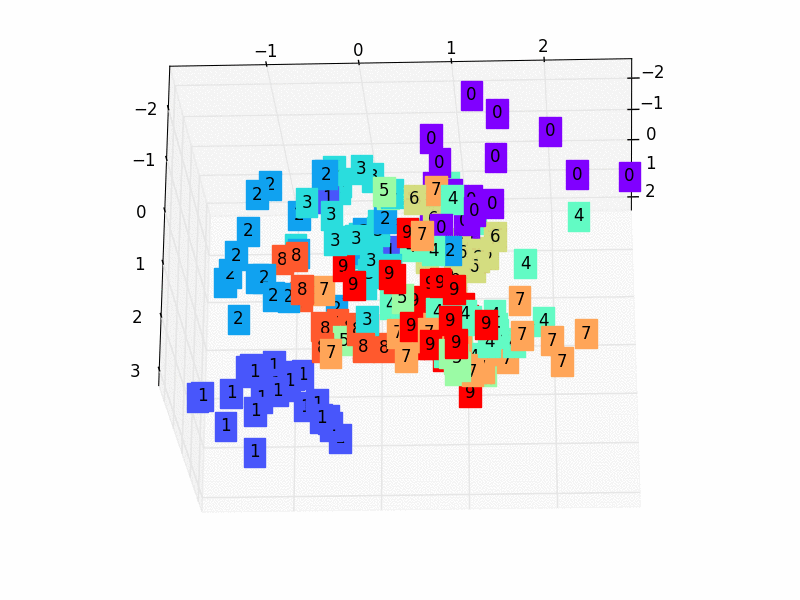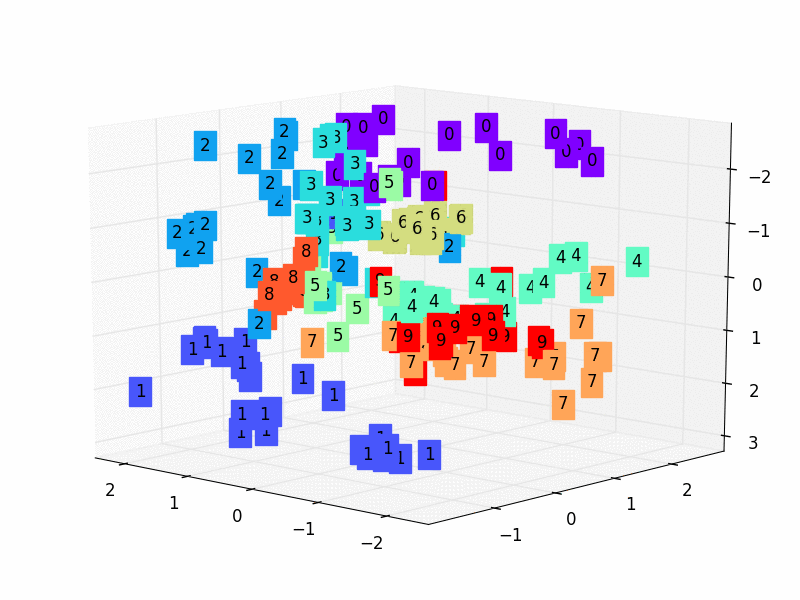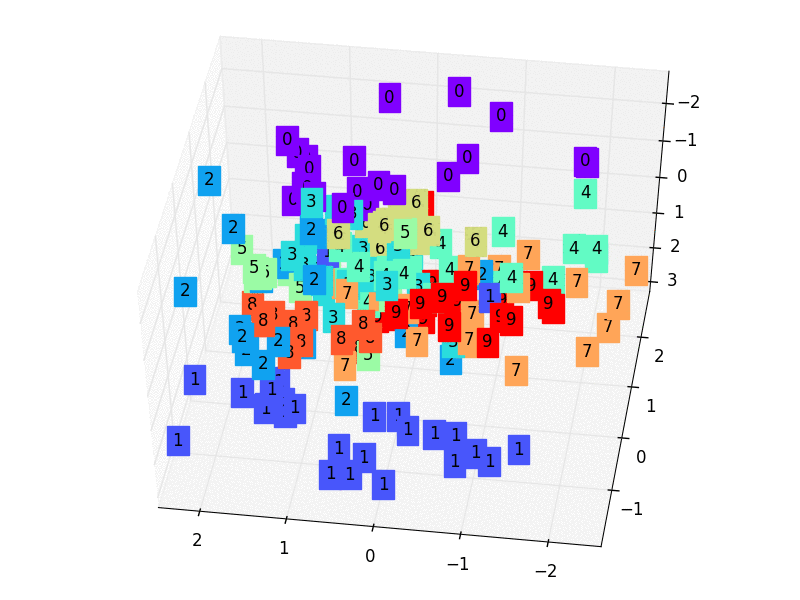
Let’s look at how to utilize an automatic encoder to reduce dimensionality now that the presentations are finished.
We’ll just project a 3-dimensional dataset onto a 2-dimensional space for simplicity’s sake. The first step in accomplishing this assignment is to create a 3D dataset. With the following code, you can accomplish it quickly in Autoencoders.
To begin, we define the encoder, which is a thick layer of two neurons that receives three-dimensional inputs (according to our dataset). As a result, we limited the latent-space representation to a dimension of two (the output of the encoder).
Then we define the decoder, which is likewise a thick layer but this time with three neurons since we want to rebuild our 3-dimensional input at the decoder’s output.
The Autoencoders is created by combining the two.
Finally, the Autoencoder determines the optimum 2D plane onto which to project the data while maintaining as much variation as feasible. Let’s look at our data projection now!
Autoencoders with Regularization
Our model will be able to learn the task of copying data in inputs without extracting crucial information if we give our network too much capacity with many hidden layers.
The Automatic encoder would be unable to learn anything in this scenario and would be overfitting.
Undercomplete AE, as well as Overcomplete AE, are both affected by this issue (when the codings have higher dimensions than the inputs).
We’d want to be able to provide our model capacity rather than limiting it to tiny networks in order to reduce the number of parameters.
We do this by employing Regularized Automatic encoders, which enable the model to generate new attributes and generalize more effectively.
There are several forms of Regularized AE, but let us look at a few examples.
Sparse Autoencoders are just AEs that have had a sparsity penalty applied to their loss function.
For example, sparse AEs are common in categorization tasks. A feedforward network with this sparsity penalty merely has a regularizer term added to it.
Denoising Autoencoders: Adding noise to the inputs (e.g., Gaussian) drives our model to learn crucial characteristics from the data.
Autoencoders with Denoising (DAE)
This Automatic encoder is an alternative to the normal notion that we just reviewed, which is prone to overfitting.
The data is partially contaminated by noises introduced to the input vector in a random way in the case of a Denoising Autoencoders. The model is then trained to predict the uncorrupted original data point as its output.
Continue Reading, just click on: https://24x7offshoring.com/blog/
Autoencoders are a type of artificial neural network that are used to learn efficient codings of unlabeled data. They are trained to reconstruct their input data as closely as possible, and this can be used for a variety of tasks, such as dimensionality reduction, image compression, and anomaly detection.
Autoencoders are typically made up of two parts: an encoder and a decoder. The encoder takes the input data and compresses it into a lower-dimensional representation. The decoder then takes this representation and reconstructs the original input data.
The encoder and decoder are typically made up of neural networks. The encoder is typically a feedforward neural network, while the decoder is typically a recurrent neural network.
Autoencoders are trained using a technique called backpropagation. Backpropagation is a method for adjusting the weights of a neural network so that it minimizes a loss function. In the case of autoencoders, the loss function is typically the mean squared error between the reconstructed input data and the original input data.
Autoencoders have been used for a variety of tasks, such as:
- Dimensionality reduction: Autoencoders can be used to reduce the dimensionality of data while preserving as much information as possible. This can be useful for tasks such as image compression and anomaly detection.
- Image compression: Autoencoders can be used to compress images by learning a lower-dimensional representation of the images. This can be useful for storing and transmitting images.
- Anomaly detection: Autoencoders can be used to detect anomalies in data by looking for data that is not well-represented by the lower-dimensional representation. This can be useful for tasks such as fraud detection and quality control.
Autoencoders are a powerful tool for learning efficient codings of unlabeled data. They have been used for a variety of tasks, and they are likely to be used for even more tasks in the future.
Autoencoders are a type of artificial neural network that are used to learn efficient codings of unlabeled data. They are trained to reconstruct their input data as closely as possible, and this can be used for a variety of tasks, such as dimensionality reduction, image compression, and anomaly detection.
Autoencoders are typically made up of two parts: an encoder and a decoder. The encoder takes the input data and compresses it into a lower-dimensional representation. The decoder then takes this representation and reconstructs the original input data.
The encoder and decoder are typically made up of neural networks. The encoder is typically a feedforward neural network, while the decoder is typically a recurrent neural network.
Autoencoders are trained using a technique called backpropagation. Backpropagation is a method for adjusting the weights of a neural network so that it minimizes a loss function. In the case of autoencoders, the loss function is typically the mean squared error between the reconstructed input data and the original input data.
Autoencoders have been used for a variety of tasks, such as:
- Dimensionality reduction: Autoencoders can be used to reduce the dimensionality of data while preserving as much information as possible. This can be useful for tasks such as image compression and anomaly detection.
- Image compression: Autoencoders can be used to compress images by learning a lower-dimensional representation of the images. This can be useful for storing and transmitting images.
- Anomaly detection: Autoencoders can be used to detect anomalies in data by looking for data that is not well-represented by the lower-dimensional representation. This can be useful for tasks such as fraud detection and quality control.
Autoencoders are a powerful tool for learning efficient codings of unlabeled data. They have been used for a variety of tasks, and they are likely to be used for even more tasks in the future.