Recognize audio information

Audio Data. Our daily lives are filled with diverse audio in the form of sounds and speeches. R eading them is now a critical challenge for various industries such as music, criminal investigation, speech reputation, etc. Audio information analysis includes exploring and interpreting sound indicators by extracting valuable insights, recognizing patterns, and making informed selections. This multifaceted area encompasses a branch of essential standards and techniques, which contribute to a deeper understanding of audio statistics. In this text, we can see different methods to understand audio information.

Audio data logs

Audio is the representation of sound as a set of electrical impulses or digital facts. It is the process of converting sound into an electrical signal that can be stored, transferred or processed. The electrical signal is then transformed into sound, which the listener can also hear.

Audio is a way of communicating our lives and affects the way we relate to and perceive the environment around us. For this implementation, we need an audio record (.wav). Let’s understand the audio data using ‘Recording.wav’, which can be downloaded immediately from here. You can use any audio document (.wav) as you see fit.

At first, we can import all 24x7offshoring libraries to analyze tunes and audio. Provides the components necessary to build tuned statistics retrieval systems.

• To understand audio data, we first want to recognize sampling and the price of sampling.

Sampling:

We will understand audio signals very correctly by sampling in which continuous analog audio signals are converted into discrete virtual values. Measures the amplitude of the audio signal at regular intervals in time.

Sampling rate:

This is the range of total samples taken per second during the analog to digital conversion process. Sampling load is measured in hertz (Hz).
Since the human voice has audible frequencies below eight kHz, sampling speech at sixteen kHz is sufficient. A faster pattern price simply increases the computing cost of processing those files.

In code, we can use the Librosa module to model audio files implicitly. It will first study the audio report and then convert it into a waveform (a string of amplitude values) that can be processed digitally.

 

Production:

Sampling Rate: 48000 Hz
The audio sampling rate used is 48000 Hz.

Listen to audio files with an identical sample rate:

Production:

Upload sampling-Geeksforgeeks

Sampling load: 4800

Concentrate Audio documents with Double Sampling charge:

Audio(waveform, price=sampling rate*2)

Production:

Sampling load: 9600

Listen to audio files at half sampling rate:

Audio(waveform, rate=sampling rate/2)

Production:

Sampling rate: 2400

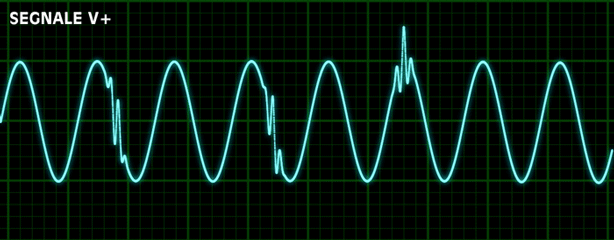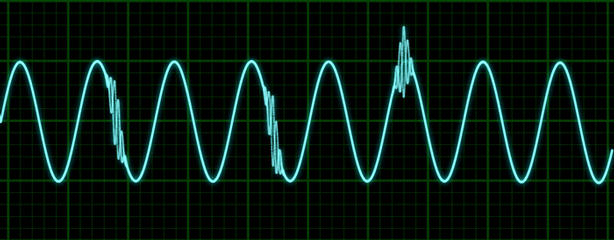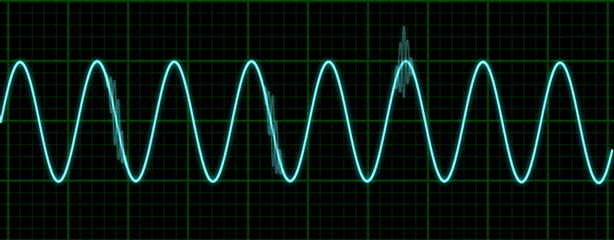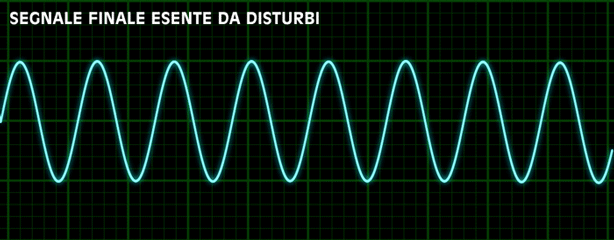
We can learn from the audio above that even when changing the sample rate, the audio is distorted.

Calculate amplitude and bit intensity

Amplitude and bit intensity are vital principles for recognizing audio signal strength.

Amplitude:

It is the intensity of an audio signal at a specific moment in time that corresponds to the height of the waveform at that moment in time. Amplitude is measured in decibels (dB). Humans perceive the amplitude of the sound wave as volume. A rock concert can be around 125 dB, which is louder than a normal voice and, outdoors, the level of human hearing.

 

Bit rate:

The precision with which this amplitude value can be described depends on the bit intensity of the sample. The virtual representation is more similar to the real continuous sound wave the better the bit intensity is. Better bitrate results, better audio, excellent. For common audio documents, the bit depth can be 8 bits, 16 bits, or 24 bits. We will print the amplitude range by subtracting the degrees of maximum amplitude and minimum amplitude.
Inside the code snippet, it calculates the amplitude range of the waveform. The soundlife library stores the audio file in the audio_data variable.

 

The line of code bit_ Depth = audio_data.dtype.itemsize calculates the bit intensity of the audio records by parsing the type information from the audio_data array and finding the length of the element in bytes.

• # Calculate the variety of amplitude
• amplitude_range = np.max(waveform) – np.min(waveform)
• # Get the bitrate of the audio records.
• audio_data, sampling_rate = sf.study(audio_file)
• bit_profundidad = audio_data.dtype.itemsize
• # print values
• print(f’Amplitude range: {amplitude_range}’)
• print(f’Bit depth: {bit_depth} bits’)

Production:

Amplitude variety: 0.292144775390625
Bit depth: 8 bits
So, our audio file is in eight bits category of bit intensity.

Understanding the amplitude range and bit intensity allows us to benefit beneficial insights into the characteristics of an audio record, that is vital in audio processing and analysis responsibilities.

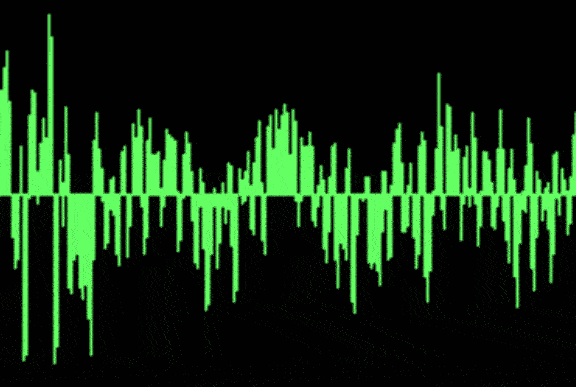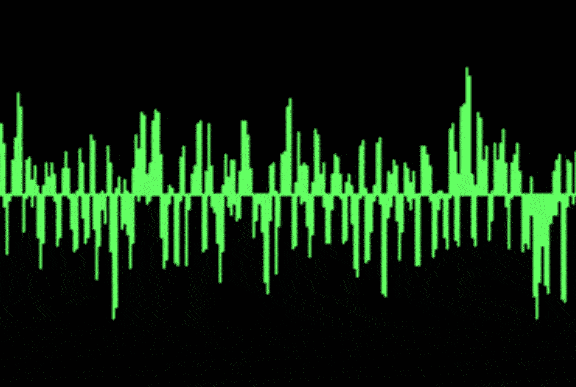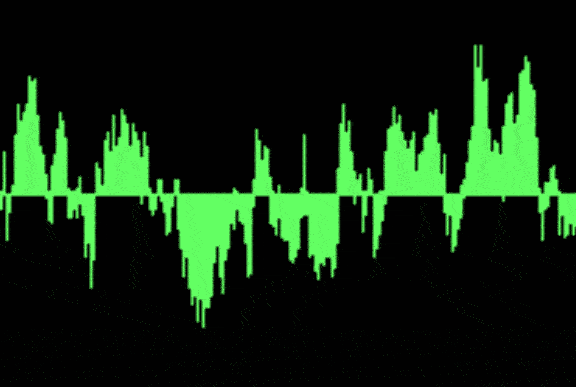
Waveform (Time domain) representation

A waveform is the graphical illustration of of an audio sign within the time area in which every point on the waveform represents the amplitude of the audio sign at a specific point in time. it’s going to assist us to understand how the audio signal varies over time through its revealing features like sound period, pauses and amplitude changes.

A waveform is the graphical illustration of an audio signal within the time area in which each point on the waveform represents the amplitude of the audio signal at a specific time.Nos ayudará a comprender cómo varía la señal de audio con el tiempo a través de sus características reveladoras como la duración del sonido, las pausas y los cambios de amplitud.

in the code snippet, we’ve got plot waveform leveraging librosa and matplotlib.

• # Plot the waveform
• ## set length
• plt.discern(figsize=(8, four))
• ## show the waveform of the adio signal
• librosa.display.waveshow(waveform, sr = sampling_rate)
• plt.xlabel(‘Time’)
• plt.ylabel(‘Amplitude’)
• plt.name(‘Audio Waveform’)
• plt.grid(real)
• plt.display()
• Output:

Audio Wavefrom-Geeksforgeeks
Waveform representation

Visualizing Frequency Spectrum

Frequency Spectrum is a illustration of ways the strength in an audio sign is distributed throughout exclusive frequencies which can be calculated with the aid of making use of a mathematical transformation like the quick Fourier remodel (FFT) to the audio signal. it’s miles very useful for figuring out musical notes, detecting harmonics or filtering unique frequency components.

The code snippet computes rapid Fourier transform and plots frequency spectrum of audio the use of matplotlib.

• # Compute the FFT of the waveform
• spectrum = fft(waveform)
• # Frequency containers
• frequencies = np.fft.fftfreq(len(spectrum), 1 / sampling_rate)
• # Plot the frequency spectrum
• plt.figure(figsize=(8, 4))
• plt.plot(frequencies[:len(frequencies)//2], np.abs(spectrum[:len(spectrum)//2]))
• plt.xlabel(‘Frequency (Hz)’)
• plt.ylabel(‘Amplitude’)
• plt.title(‘Frequency Spectrum’)
• plt.grid(proper)
• plt.display()
  Output:

Screenshot-2023-10-06-162203
Frequency Spectrum

The plot displays the frequency of the audio sign, which lets in us to have a look at the dominant frequencies and their amplitudes.

Spectrogram

Spectrogram is a time-frequency representation of an audio sign which provides a 2d visualization of ways the frequency content material of the audio sign changes through the years.

 

In spectrogram, the darkish areas imply less presence of a frequency and inside the other hand brilliant regions suggest strong presence of a frequency at a sure time. this may assistance is numerous responsibilities like speech reputation, musical analysis and identifying sound styles.

The code snippet computes and plots the audio waveform the usage of matplotlib library and scipy.sign.spectrogram function. inside the code, epsilon defines a small regular to avoid department by using zero. Epsilon is delivered to the spectrogram values earlier than taking logarithm to prevent issues with very small values.

• # Compute the spectrogram
• # Small constant to avoid department by using zero(if any)
• epsilon = 1e-forty
• f, t, Sxx = spectrogram(waveform, fs=sampling_rate)
• # Plot the spectrogram with the steady delivered to Sxx
• plt.figure(figsize=(eight, 4))
• plt.pcolormesh(t,f,10*np.log10(Sxx+epsilon));
• plt.colorbar(label=’power/Frequency (dB/Hz)’)
• plt.xlabel(‘Time (s)’)
• plt.ylabel(‘Frequency (Hz)’)
• plt.name(‘Spectrogram’)
• plt.show()

Output:

Screenshot-2023-10-06-162421-min
Spectrogram

The plot displays spectrogram, which represents how the frequencies within the audio signal trade over time. The color intensity represents whether or not the frequency is excessive or low at each time point.

Conclusion

we are able to conclude that diverse kinds of visualization responsibilities assist us to recognize the behavior of audio signals very efficaciously. also knowledge audio signal may be very important task for audio classification, tune style category and velocity reputation.

And why pass anywhere else when our DSA to development: Coding manual helps you do this in a unmarried program! observe now to our DSA to improvement software and our counsellors will connect to you for in addition steerage & help.

Advent to audio statistics

With the aid of nature, a valid wave is a non-stop signal, meaning it consists of an endless wide variety of sign values in a given time. This poses issues for digital gadgets which assume finite arrays. To be processed, stored, and transmitted through digital devices, the non-stop sound wave needs to be converted into a series of discrete values, known as a virtual representation.

In case you examine any audio dataset, you’ll find virtual documents with sound excerpts, which include text narration or song. you could stumble upon exclusive document formats which includes .wav (Waveform Audio report), .flac (loose Lossless Audio Codec) and .mp3 (MPEG-1 Audio Layer three). these codecs in particular fluctuate in how they compress the virtual illustration of the audio signal.

Permit’s take a look at how we arrive from a non-stop sign to this illustration. The analog sign is first captured by means of a microphone, which converts the sound waves into an electrical signal. the electrical sign is then digitized by using an Analog-to-digital Converter to get the virtual representation via sampling.

Sampling and sampling charge
Sampling is the process of measuring the price of a continuous sign at constant time steps. The sampled waveform is discrete, since it consists of a finite quantity of sign values at uniform durations.

Sign sampling illustration
instance from Wikipedia article: Sampling (signal processing)

The sampling fee (also referred to as sampling frequency) is the wide variety of samples taken in a single 2d and is measured in hertz (Hz). to give you a point of reference, CD-fine audio has a sampling price of forty four,100 Hz, that means samples are taken 44,a hundred instances in step with 2d. For contrast, high-decision audio has a sampling rate of 192,000 Hz or 192 kHz. A commonplace sampling fee utilized in schooling speech models is 16,000 Hz or 16 kHz.

The choice of sampling fee in the main determines the very best frequency that can be captured from the signal. that is additionally called the Nyquist restrict and is precisely 1/2 the sampling price. The audible frequencies in human speech are underneath 8 kHz and consequently sampling speech at 16 kHz is sufficient. the usage of a higher sampling fee will now not capture greater facts and simply leads to an boom within the computational value of processing such files. on the other hand, sampling audio at too low a sampling rate will result in information loss. Speech sampled at eight kHz will sound muffled, because the higher frequencies cannot be captured at this charge.

It’s essential to make certain that all audio examples to your dataset have the same sampling charge while running on any audio task. in case you plan to apply custom audio statistics to nice-music a pre-trained model, the sampling rate of your facts have to in shape the sampling charge of the information the version become pre-skilled on.

The samplingprice determines the time c language between successive audio samples, which impacts the temporal decision of the audio records. don’t forget an instance: a five-second sound at a sampling fee of 16,000 Hz may be represented as a chain of 80,000 values, at the same time as the identical 5-second sound at a sampling price of 8,000 Hz can be represented as a sequence of 40,000 values.

Transformer fashions that solve audio responsibilities deal with examples as sequences and rely on interest mechanisms to learn audio or multimodal illustration. when you consider that sequences are unique for audio examples at special sampling costs, it is going to be hard for models to generalize between sampling fees. Resampling is the method of creating the sampling prices fit, and is a part of preprocessing the audio information.

Amplitude and bit intensity even as the sampling fee tells you how regularly the samples are taken, what exactly are the values in every sample?

Sound is made via adjustments in air pressure at frequencies which are audible to human beings. The amplitude of a valid describes the sound pressure level at any given immediate and is measured in decibels (dB). We perceive the amplitude as loudness. to provide you an example, a ordinary talking voice is under 60 dB, and a rock concert can be at round 125 dB, pushing the limits of human listening to.

In digital audio, each audio sample information the amplitude of the audio wave at a point in time. The bit depth of the sample determines with how lots precision this amplitude cost may be defined. The higher the bit intensity, the more faithfully the digital illustration approximates the authentic continuous sound wave.

The most common audio bit depths are sixteen-bit and 24-bit. every is a binary term, representing the number of viable steps to which the amplitude fee may be quantized whilst it’s transformed from non-stop to discrete: 65,536 steps for 16-bit audio, a whopping 16,777,216 steps for twenty-four-bit audio. because quantizing entails rounding off the non-stop cost to a discrete cost, the sampling procedure introduces noise. The higher the bit depth, the smaller this quantization noise. In practice, the quantization noise of 16-bit audio is already small sufficient to be inaudible, and using higher bit depths is usually no longer necessary.

You could also come upon 32-bit audio. This shops the samples as floating-point values, whereas sixteen-bit and 24-bit audio use integer samples. The precision of a 32-bit floating-point fee is 24 bits, giving it the same bit intensity as 24-bit audio. Floating-point audio samples are expected to lie inside the [-1.0, 1.0] variety. in view that device gaining knowledge of fashions naturally paintings on floating-factor records, the audio should first be converted into floating-point layout earlier than it is able to be used to train the model. We’ll see the way to do that inside the subsequent phase on Preprocessing.

Just as with non-stop audio indicators, the amplitude of digital audio is usually expressed in decibels (dB). on account that human listening to is logarithmic in nature — our ears are greater sensitive to small fluctuations in quiet sounds than in loud sounds — the loudness of a sound is easier to interpret if the amplitudes are in decibels, which can be also logarithmic.

The decibel scale for actual-world audio begins at 0 dB, which represents the quietest possible sound people can hear, and louder sounds have larger values. but, for virtual audio alerts, 0 dB is the loudest viable amplitude, at the same time as all different amplitudes are negative. As a quick rule of thumb: every -6 dB is a halving of the amplitude, and something underneath -60 dB is typically inaudible except you certainly crank up the extent.

Audio as a waveform

You can have visible sounds visualized as a waveform, which plots the sample values through the years and illustrates the modifications inside the sound’s amplitude. that is also referred to as the time area representation of sound.

Audio Compressor – best Ways to Reduce audio size audio quality reducer

This type of visualization is useful for identifying particular functions of the audio sign which include the timing of man or woman sound events, the overall loudness of the signal, and any irregularities or noise gift in the audio.

Waveform plot

This plots the amplitude of the sign at the y-axis and time alongside the x-axis. In different words, every point corresponds to a unmarried pattern cost that changed into taken while this sound become sampled. also observe that librosa returns the audio as floating-point values already, and that the amplitude values are indeed in the [-1.0, 1.0] variety.

This plots sign amplitude on the y-axis and time along the x-axis.En otras palabras, cada punto corresponde a un solo costo de patrón que se tomó mientras se sampleaba este sonido. También observe que librosa ya devuelve el audio como valores de punto flotante, y que los valores de amplitud están de hecho en la variedad [-1.0, 1.0].

Visualizing the audio together with taking note of it could be a useful tool for expertise the records you are working with. you could see the form of the signal, look at patterns, discover ways to spot noise or distortion. in case you preprocess information in some methods, together with normalization, resampling, or filtering, you may visually verify that preprocessing steps had been implemented as predicted. After education a version, you may additionally visualize samples in which mistakes occur (e.g. in audio type challenge) to debug the difficulty.

The frequency spectrum

any other way to visualise audio information is to plan the frequency spectrum of an audio sign, additionally known as the frequency area illustration. The spectrum is computed the use of the discrete Fourier remodel or DFT. It describes the individual frequencies that make up the sign and the way sturdy they’re.

Another way to visualize audio data is to plan the frequency spectrum of an audio signal, also known as frequency area representation. The spectrum is calculated by using discrete Fourier remodeling or DFT. Describe the individual frequencies that make up the sign and how strong they are.

Allow’s plot the frequency spectrum for the identical trumpet sound by taking the DFT the use of numpy’s rfft() characteristic. even as it’s far viable to devise the spectrum of the entire sound, it’s more beneficial to look at a small area as an alternative. right here we’ll take the DFT over the first 4096 samples, which is roughly the length of the first be aware being performed:

Copied
import numpy as np

numpy as np

dft_input = array[:4096]

# calculate the DFT

window = np.hanning(len(dft_input))

windowed_input = dft_input * window

dft = np.fft.rfft(windowed_input)

# get the amplitude spectrum in decibels
amplitude = np.abs(dft)

amplitud = np.abs(dft)

amplitude_db = librosa.amplitude_to_db(amplitude, ref=np.max)

amplitude_db = bookkeeper.amplitude_to_db(amplitude, ref=np.max);

# get the frequency boxes

frequency = librosa.fft_frequencies(sr=sampling_rate, n_fft=len(dft_input))

frecuencia = librosa.fft_frequencies(sr=sampling_rate, n_fft=len(dft_input))

• plt.determine().set_figwidth(12)
• plt.plot(frequency, amplitude_db)
• plt.xlabel(“Frequency (Hz)”)
• plt.ylabel(“Amplitude (dB)”)
• plt.xscale(“log”)

Spectrum plot

This plots the energy of the diverse frequency components which can be found in this audio phase. The frequency values are at the x-axis, generally plotted on a logarithmic scale, whilst their amplitudes are on the y-axis.

The frequency spectrum that we plotted suggests several peaks. those peaks correspond to the harmonics of the observe that’s being played, with the better harmonics being quieter. for the reason that first height is at round 620 Hz, that is the frequency spectrum of an E♭ notice.

The output of the DFT is an array of complicated numbers, made up of real and imaginary components. Taking the magnitude with np.abs(dft) extracts the amplitude information from the spectrogram. The attitude between the real and imaginary additives provides the so-called segment spectrum, however this is regularly discarded in machine studying programs.

You used librosa.amplitude_to_db() to transform the amplitude values to the decibel scale, making it less difficult to peer the finer information in the spectrum. once in a while humans use the electricity spectrum, which measures strength in place of amplitude; that is genuinely a spectrum with the amplitude values squared.

In exercise, human beings use the term FFT interchangeably with DFT, because the FFT or fast Fourier transform is the handiest green manner to calculate the DFT on a pc.
The frequency spectrum of an audio signal consists of the precise same statistics as its waveform — they’re surely one of a kind approaches of searching at the same records (here, the primary 4096 samples from the trumpet sound). where the waveform plots the amplitude of the audio signal through the years, the spectrum visualizes the amplitudes of the man or woman frequencies at a set factor in time.

The frequency spectrum of an audio signal consists of exactly the same data as its waveform; surely they are different ways of searching the same records (here, the first 4096 samples of the trumpet sound). While the waveform traces the amplitude of the audio signal over years, the spectrum visualizes the amplitudes of individual frequencies over a given time factor.

Spectrogram

What if we need to see how the frequencies in an audio sign change? The trumpet plays several notes and all of them have one-of-a-kind frequencies. The problem is that the spectrum simplest indicates a frozen picture of the frequencies at a given immediately. the solution is to take a couple of DFTs, every masking simplest a small slice of time, and stack the ensuing spectra collectively right into a spectrogram.

What if we need to see how frequencies change in an audio signal? The trumpet plays several notes and they all have unique frequencies. The problem is that the spectrum only indicates a frozen image of the frequencies at a given instant. The solution is to take a pair of DFTs, each masking only a small portion of time, and stack the resulting spectra into a spectrogram.

A spectrogram plots the frequency content material of an audio signal because it modifications through the years. It allows you to see time, frequency, and amplitude all on one graph. The set of rules that performs this computation is the STFT or quick Time Fourier rework.

The spectrogram is one of the most informative audio tools available to you. as an example, when working with a music recording, you can see the numerous contraptions and vocal tracks and the way they contribute to the general sound. In speech, you may become aware of distinctive vowel sounds as each vowel is characterised with the aid of unique frequencies.

Allow’s plot a spectrogram for the same trumpet sound, using librosa’s stft() and specshow() capabilities:

Copied

import numpy as np

numpy as np

D = bookkeeper.stft(array)

S_db = bookkeeper.amplitude_to_db(np.abs(D), ref=np.max);

S_db = librosa.amplitude_to_db(np.abs(D), ref=np.max)

plt.figure().set_figwidth(12)

librosa.show.specshow(S_db, x_axis=”time”, y_axis=”hz”)

librosa.show.specshow(S_db, x_axis=”time”, y_axis=”hz”)

plt.colorbar()

plt.colorbar()
Spectrogram plot

Spectrogram graph

on this plot, the x-axis represents time as in the waveform visualization but now the y-axis represents frequency in Hz. The intensity of the colour offers the amplitude or energy of the frequency factor at each factor in time, measured in decibels (dB).

In this graph, the x-axis represents time as in the waveform display, but now the y-axis represents frequency in Hz. Color intensity provides the amplitude or energy of the frequency factor at each factor over time, measured in decibels (dB).

The spectrogram is created via taking quick segments of the audio signal, typically lasting a few milliseconds, and calculating the discrete Fourier remodel of every phase to gain its frequency spectrum. The ensuing spectra are then stacked collectively on the time axis to create the spectrogram. each vertical slice on this picture corresponds to a unmarried frequency spectrum, visible from the top. by using default, librosa.stft() splits the audio signal into segments of 2048 samples, which offers a good exchange-off between frequency resolution and time decision.

For the reason that spectrogram and the waveform are specific perspectives of the identical data, it’s viable to turn the spectrogram again into the original waveform the use of the inverse STFT. however, this requires the phase facts in addition to the amplitude information. If the spectrogram become generated by a system mastering version, it commonly most effective outputs the amplitudes. if so, we are able to use a segment reconstruction set of rules which includes the conventional Griffin-Lim algorithm, or the usage of a neural network referred to as a vocoder, to reconstruct a waveform from the spectrogram.

Spectrograms aren’t just used for visualization. Many device studying fashions will take spectrograms as input — rather than waveforms — and produce spectrograms as output.

Now that we realize what a spectrogram is and how it’s made, allow’s take a look at a variant of it widely used for speech processing: the mel spectrogram.

Mel spectrogram

A mel spectrogram is a variation of the spectrogram this is usually used in speech processing and gadget mastering duties. it’s miles similar to a spectrogram in that it shows the frequency content of an audio signal through the years, however on a different frequency axis.

A Mel spectrogram is a variation of the spectrogram typically used in speech processing and device mastery tasks. It is similar to a spectrogram in that it shows the frequency content of an audio signal over years, but on a different frequency axis.

In a general spectrogram, the frequency axis is linear and is measured in hertz (Hz). however, the human auditory machine is greater sensitive to adjustments in lower frequencies than better frequencies, and this sensitivity decreases logarithmically as frequency increases. The mel scale is a perceptual scale that approximates the non-linear frequency reaction of the human ear.

To create a mel spectrogram, the STFT is used just like earlier than, splitting the audio into short segments to attain a chain of frequency spectra. moreover, each spectrum is sent via a fixed of filters, the so-referred to as mel filterbank, to transform the frequencies to the mel scale.

Permit’s see how we can plot a mel spectrogram the usage of librosa’s melspectrogram() feature, which performs all of those steps for us:

Copied
S = librosa.function.melspectrogram(y=array, sr=sampling_rate, n_mels=128, fmax=8000)

S = librosa.function.melspectrogram(y=array, sr=sampling_rate, n_mels=128, fmax=8000)
S_dB = librosa.power_to_db(S, ref=np.max)

S_dB = librosa.power_to_db(S, ref=np.max)

plt.determine().set_figwidth(12)

librosa.show.specshow(S_dB, x_axis=”time”, y_axis=”mel”, sr=sampling_rate, fmax=8000)

plt.colorbar()

Mel spectrogram plot

In the instance above, n_mels stands for the quantity of mel bands to generate. The mel bands define a set of frequency levels that divide the spectrum into perceptually meaningful

additives, using a hard and fast of filters whose shape and spacing are chosen to imitate the way the human ear responds to one-of-a-kind frequencies. not unusual values for n_mels

are 40 or eighty. fmax shows the highest frequency (in Hz) we care about.

Simply as with a normal spectrogram, it’s not unusual practice to explicit the electricity of the mel frequency components in decibels. this is generally called a log-mel spectrogram, because the conversion to decibels includes a logarithmic operation. The above example used librosa. Power_to_db() as librosa. Characteristic.melspectrogram() creates a electricity spectrogram.

Developing a mel spectrogram is a lossy operation because it entails filtering the sign. changing a mel spectrogram back into a waveform is more difficult than doing this for a regular spectrogram, because it calls for estimating the frequencies that have been thrown away. this is why system learning fashions together with HiFiGAN vocoder are needed to produce a waveform from a mel spectrogram.

As compared to a preferred spectrogram, a mel spectrogram can seize greater significant capabilities of the audio signal for human belief, making it a famous choice in obligations inclusive of speech reputation, speaker identity, and music style class.

Now that you know how to visualize examples of audio data, go ahead and try to see what your favorite sounds look like.